今回のテーマは「音程」です。
保育士試験の音楽の筆記問題で、
毎年かならず出題される
「完全●度下へ」とか「長●度上へ」という問題。
この度数であらわす「~度」のことを
「音程」といいます。
ざっくり言えば、
「音と音がどれくらい離れているか」
という間隔を表します。
音の高さを変える、
調を変える、
コードネームを変える・・・
あらゆる場面で「度数」「音程」が必要です。
現在の筆記問題でも、
問4と問5では、
ほぼ毎年のように出題されています。
この度数を攻略することによって、
音楽の筆記問題がだいぶラクになります。
度数の表しかた、数え方を
しっかり押さえて、
コワイ問題が無くなるように解説していきますね!
音程とは
ある2つの音の間隔(つまり離れぐあい)を
「音程」といいます。
音程は
度数(数字)+ 響きの種類を表す文字(完全、長、短など)
の組み合わせで表します。
音程が連続すると
➡ メロディになる
複数の音程を組み合わせると
➡ ハーモニーやコードになる
このように、
音程は音楽に欠かせない要素なのです。
覚えるべき「度数」とは
音楽にはあらゆる度数があります。
一番小さい「1度」から
・・・・・・無限ですね(笑)
ここでは、
試験勉強をする皆さんの負担が少しでも軽くなるように、
保育士試験に出る範囲にしぼって解説します。
これまでの過去問では、
2度、3度、4度、5度が出されています。
それ以上の度数が出る可能性もありますが、
保育の現場で考えると、
そこまで大幅に移調する機会もありません。
ということで、基本的な1度を加えて、
2~5度について覚えると良いと思います。
※余裕があれば、
ぜひ6~8度についても触れて下さいね。
度数の表しかた
♯や♭が何もつかない音(幹音といいます)どうしの音程が
基本になります。
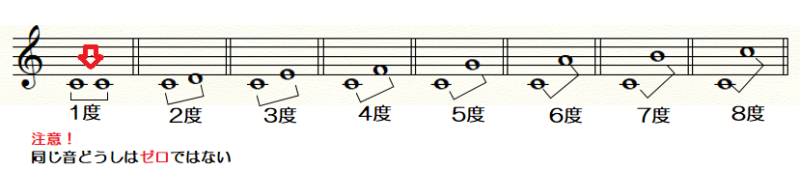
同じ音どうしはゼロではなく「1度」です。
ひとつ音が離れるごとに、
2度、3度・・・と数字が大きくなります。
これをピアノの鍵盤で見てみましょう。
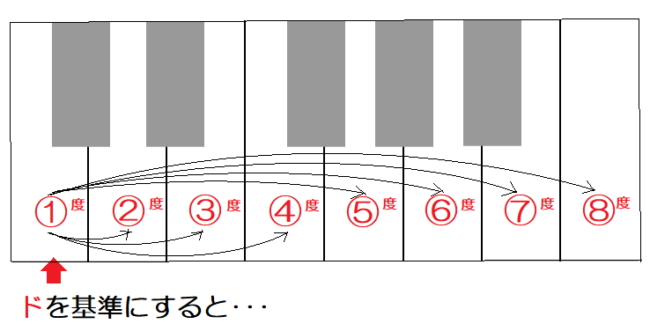
鍵盤がひとつ離れるごとに、
度数が増えていきます。
この関係は、
他の音を基準にしても当てはまります。

ここで「度数」を数えるポイントをまとめます。
「レ~ソ」はレミファソ・・・のように、
2音の間にある音すべての数が「度数」になる。
(ドレミ → 3度、レミファソ → 4度)
・2音のどちらかの音を基準にして、
間にあるすべての白い鍵盤の数が「度数」になる。
(注意:基準になる音も含めて数える)
度数ごとの「響き」の種類
保育士試験に出る
2~5度について解説していきます。
※1度についても、
基礎知識として触れますね。
音の響きは、振動数の比によって、
「完全に協和する音程」
「不完全協和な音程」
「不協和な音程」に分けられます。
今まで見てきた「度数」ごとに、
その種類を紹介します。
1度 ➡ 完全協和する音程
・・・ 同じ音どうしだもんネ!
2度 ➡ 不協和な音程
・・・ 隣りどうしだからぶつかり合っちゃう?
3度 ➡ 不完全協和な音程
・・・ 不完全なのね、ザンネン
4度・5度 ➡ 完全協和する音程
・・・ イエイ!! やった~!
この響きかたの違いを、文字で表します。
・「長・短」➡ 2度、3度の響きをあらわす
※「増・減」➡ 全ての度数で使われますが、
保育士試験では扱いません。
この響きの種類を、
先ほどの「度数」と合わせて、
完全4度とか、長3度とか、短2度、完全5度
・・・などと表現します。
ここで大事なのは、
「完全」チームと「長・短」チームが
混ざらないこと。
2度と3度「にいさん(兄さん)」は、
気が長い?短い?と覚えても良いかと!
もう一度、まとめます。
※ここから変化する音程はたくさんありますが、
保育士試験ではこれだけ覚えれば良し!!
(1度 ➡ 完全1度)
2度 ➡ 長2度、短2度
3度 ➡ 長3度、短3度
4度 ➡ 完全4度
5度 ➡ 完全5度
保育士試験で出される「音程」
完全1度とは
1度の音程に関しては、
過去問では一回も出題されていませんが、
音程の基礎として触れておきます。
1度は・・・同じ音どうしの音程でしたね。
「完全」がついて「完全1度」というと、
「全く同じ音どうし」という意味になります。
同じ音どうしでも、
片方に♯や♭がつくと音の響きが変わるので、
「完全」音程ではなくなります。

上の譜例で見ていきましょう。
①は「ド」と「ド」で、
鍵盤の場所も同じですね。
これが「完全1度」です。
②は両方のもともとの音は「ド」です。
しかし片方に#が付くと
「同じ音どうし」ではなくなるので
「完全」では無くなります。
③は「ド」に♯がついていますが、
両方に付いているので、
同じ「ド#」どうしで「完全」になります。
④は「ラ」どうしで「完全1度」ですね。
⑤は・・・鍵盤上では同じ音になります。
→「異名同音」と言いましたね。
・・・徹底講座④を参照
じゃあ、
鍵盤で同じ場所の音どうしだから「完全1度」では?
と、思いがちですが・・・
前の章「度数の表しかた」で、
「♯や♭が何もつかない音(幹音といいます)どうしの音程」が
基本と学びましたね。
なので、⑤の音から♯や♭を取った音が
もともとの音程となるので、
「ラ」と「シ」は2度です。
何やら難しい「重増」というのが付いていますが、
これは保育士試験には出ません。
鍵盤上で同じ音であっても、
「異名同音」は「全く同じ音ではない」
を押さえておきましょう。
⑥は、同じ「ド」ですが・・・「高さ」が違います。
鍵盤上でも、かなり離れたところにありますよね。
1オクターブは「8度」となります。
長2度・短2度の違いとは
2度音程は保育士試験に出るので、
しっかり覚えましょう!!
2度とは、#や♭が付いていない状態の音(幹音)で、
隣り合っている音どうしの音程です。

上記の譜例①は、
全てとなりどうしの音なので「2度」です。
しかし同じ2度でも、
音どうしの距離が違うため、響きも異なります。
その響きの違いを「長・短」で区別します。

距離が長い方が「長」、
短い方が「短」となっています。
この距離が長い、短いってどういうこと?
そこで、
今度はピアノの鍵盤で距離の違いを見ていきます。
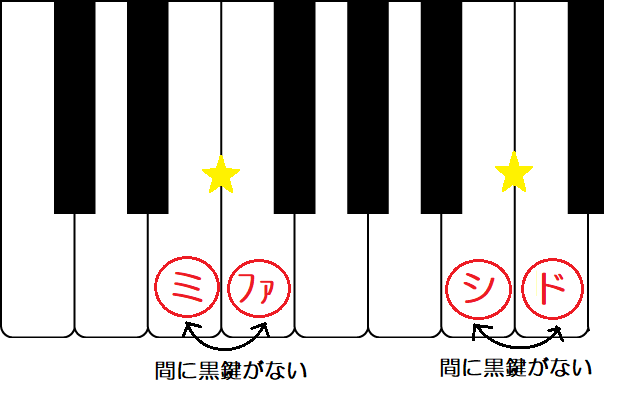
「ドーレ」「レーミ」
および「ファーソ」「ソーラ」「ラーシ」は、
間に黒い鍵盤があります。
それに対して「ミーファ」「シード」の間には
黒い鍵盤がなく、
ピッタリとくっついています。
2音の間に黒い鍵盤が無い分、
距離が短くなっているのです。
「実際のとなりの音」を、
ピアノの鍵盤で確認します。
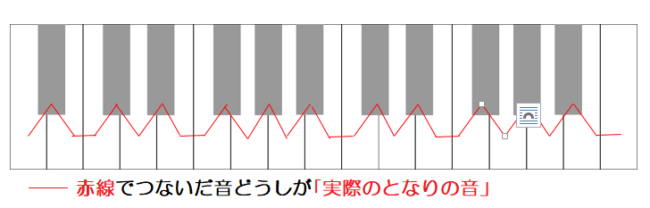
「音程」の度数は、
♯や♭を外した音で考えるのですが、
実際の音どうしの距離は、
黒と白の鍵盤をすべて含んだ、
となりどうしの音がいくつあるか、
で決まります。
まとめると、
長2度 ➡ 鍵盤の数が 3つ
短2度 ➡ 鍵盤の数が 2つ
この「鍵盤の数」をしっかり覚えておくと、
どちらかの音(または両方)に
♯や♭がついた場合もラクになります。
では、例題を見ていきましょう。

①~⑦の2度音程をみていきます。
まず、大前提となる「音程」は、
♯や♭を取って考えるので、
すべて「2度」ですね。
次に響きの種類「長か短か」は、
その2音に鍵盤の数がいくつ含まるか、
で決まります。
長2度 ➡ 鍵盤3つ
短2度 ➡ 鍵盤2つ でしたね。
①の2度は「ド#」と「レ」
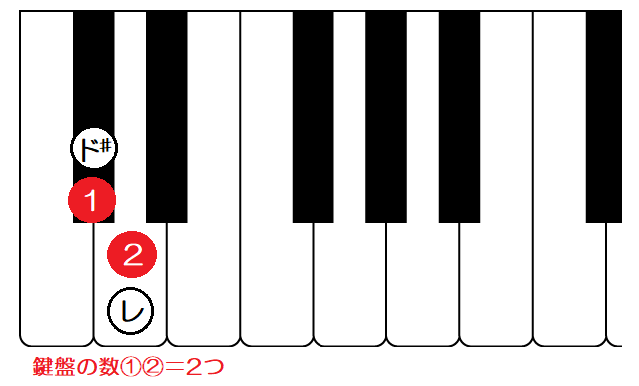
ドに♯がついたので、
「ド#~レ」までの鍵盤数は2つ=「短2度」となります。
③は「ミ」と「ファ♯」です。
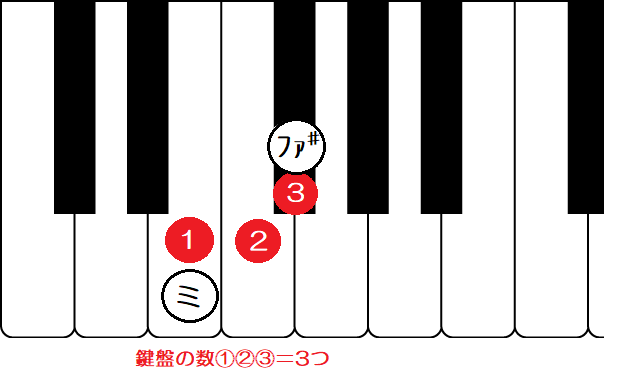
「ミ~ファ♯」 の鍵盤数は3つ=「長2度」です。
続けて
④~⑦についても鍵盤の数をみていきましょう。
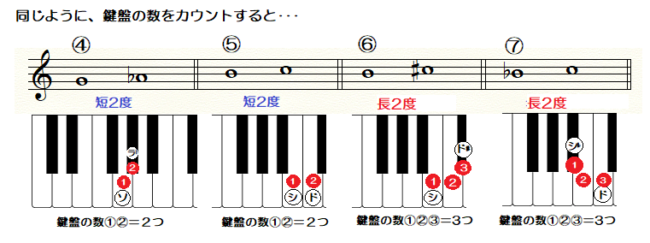
①♯や♭を除いた音で「度数」を出す。
②ピアノの鍵盤の数をカウントする。
鍵盤の数3つ ➡ 長2度
鍵盤の数2つ ➡ 短2度
長3度・短3度の違いとは
3度の音程も、
保育士試験にちょくちょく出題されています。
3度も、
2度と同じように「長・短」の響きの種類で表されます。
♯や♭を外した幹音で「3度」を見分けた後、
やはり「ピアノの鍵盤の数」をカウントして
「長・短」を区別します。
長3度 ➡ 鍵盤の数5つ
短3度 ➡ 鍵盤の数4つ
だんだん鍵盤の数が増えるので、
間違えないようにカウントしましょう。

2度の考え方と同じで、
同じ3度でも、
場所によって鍵盤の数が異なるので
「長と短」に分かれます。
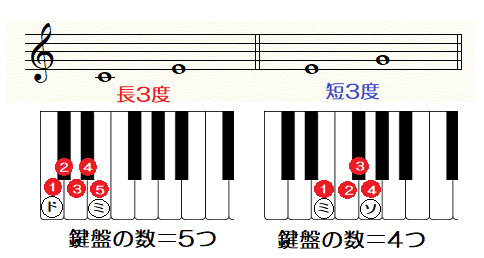
ここで気をつけたいのは、
白い鍵盤と黒い鍵盤を
もれなく全てカウントすることです。
飛ばしてカウントすると、
間違えてしまいますので、
ジグザグと・・・全部をカウントして下さいね。
では、
♯や♭がついて変化した場合も見ていきましょう。
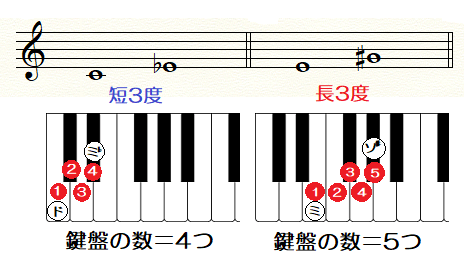
音程の考え方は、2度の時と同じです。
①まず、
♯や♭を外して「度数」を確定します ➡「3度」
②2つの音から音まで、
含まれる鍵盤の数をカウントします。
③鍵盤の数5つ ➡ 長3度
鍵盤の数4つ ➡ 短3度
完全4度とは
4度についても、保育士試験に良く出てきます。
4度は、響きの種類が「完全」でしたね。
では、どういう状態が「完全4度」なのか、
まずは♯や♭が付かない
幹音の状態を見ていきましょう。

あれ?
「ファーシ」の組み合わせだけ「増4度」?
そうなんです。
2音間に含まれるピアノの鍵盤をカウントすると・・・
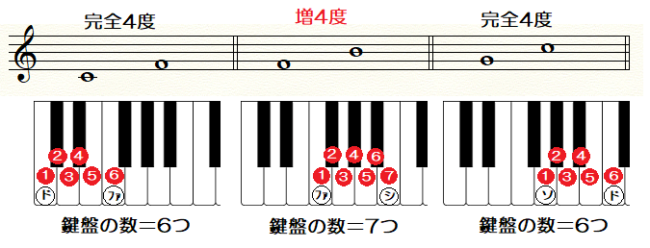
「ファーシ」 の組み合わせだけ「7つ」、
あとの組み合わせは全て「6つ」です。
このように、
完全4度 ➡ 鍵盤の数6つ です。
同じ4度でも、鍵盤の数が5つとか7つ・・・は、
「完全4度ではない」と覚えましょう。
ちなみに・・・
「ファーシ」の組み合わせに
♯や♭をつけて「鍵盤6つ」に整えると、
「完全4度」になります。
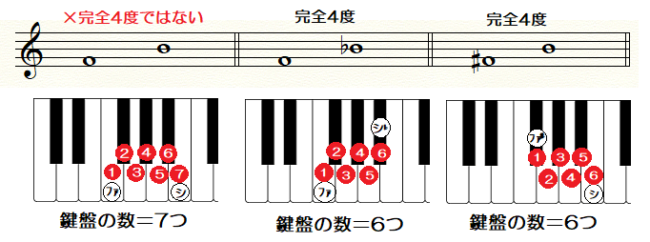
①まず、
♯や♭を外して「度数」を確定します ➡「4度」
②2つの音から音まで、
含まれる鍵盤の数をカウントします。
③鍵盤の数6つ ➡ 完全4度
完全5度とは
5度についても良く出題されていますので、
覚えていきましょう。
5度は、
1度・4度と同じ「完全」の響きを持つのでしたね。
では、
どういう状態が「完全5度」なのか、
まずは♯や♭が付かない
幹音の状態を見ていきましょう。

あれ?
「シーファ」の組み合わせだけ「減5度」??
なんだか、
4度の時と似たような状況ですね。
ピアノの鍵盤の位置によって、
ビミョーに距離が違うのです。
2音間に含まれるピアノの鍵盤を
カウントしてみましょう。
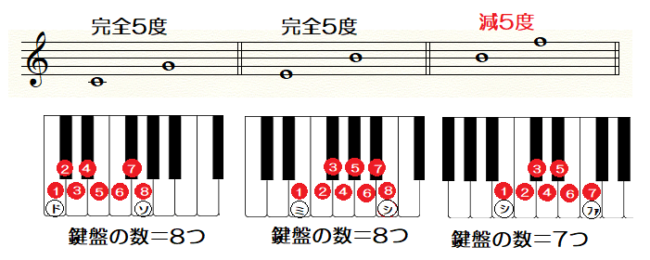
「シーファ」の組み合わせだけ「7つ」、
あとの組み合わせは全て「8つ」です。
このように、
完全5度 ➡ 鍵盤の数8つ です。
同じ5度でも、
鍵盤の数が7つとか9つ・・・は、
「完全5度ではない」と覚えましょう。
ちなみに・・・
「シーファ」の組み合わせに
♯や♭をつけて「鍵盤8つ」に整えると、
「完全5度」になります。
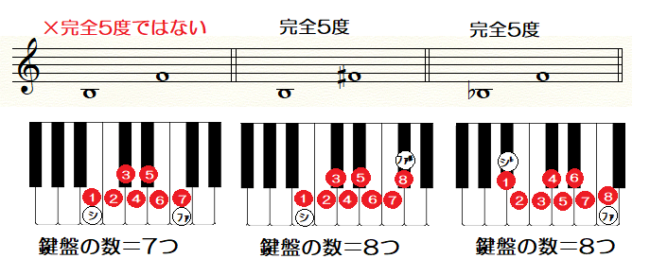
①まず、
♯や♭を外して「度数」を確定します ➡「5度」
②2つの音から音まで、
含まれる鍵盤の数をカウントします。
③鍵盤の数8つ ➡ 完全5度
注意:鍵盤の数が同じでも、音程が同じとは限らない
2度~5度について、
2音に含まれる「鍵盤の数をカウント」する方法で、
音程を探してきました。
ここで気をつけたいのが、
鍵盤の数が同じ ➡ 音程が同じとは限らない
ということです。
例を見ながら解説していきましょう。
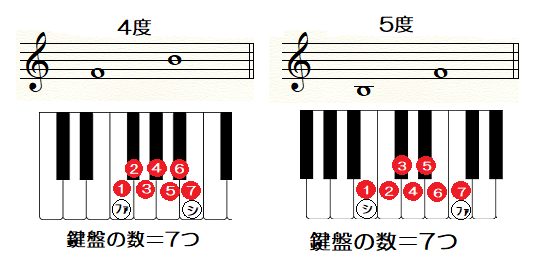
上の譜面では、
両方とも同じ「鍵盤の数=7つ」です。
では、
同じ音程なのかな?と勘違いしないように。
度数は「4度」と「5度」と異なります。
先に「鍵盤の数」をカウントすると、
間違いの元になってしまいます。
ポイントは、一番先に
♯や♭を外した音(幹音)で度数を出す
です。
ちなみに・・・
鍵盤7つの4度は「増4度」、
鍵盤7つの5度は「減5度」です。
どちらも保育士試験には出されませんが、
音程の導きかたとして「度数」から、
というポイントを押さえて下さいね!
まとめ 保育士試験に出る「音程」を覚えよう
音楽には、無限の「音程」があります。
しかし、
ここでは保育士試験に出る「音程」に絞って解説しました。
① 度数の求めかた
・♯や♭が付いていたら外して考え、
片方の音から、その音を含めて
白い鍵盤「ドレミファソラシド」の数を数える。
例:「レ~ソ」は「レミファソ」と数える ➡ 4度
「ミ~シ」は「ミファソラシ」と数える ➡ 5度
②響きの種類を覚える
(保育士試験に出る範囲にしぼります)
2度 ➡ 長2度、短2度
3度 ➡ 長3度、短3度
4度 ➡ 完全4度
5度 ➡ 完全5度
③音程を「ピアノの鍵盤の数」でカウントして導く。
(2音の間にある白黒の鍵盤すべて)
| 度数 | 鍵盤の数 | 度数 | 鍵盤の数 |
| 短2度 | 2つ | 長2度 | 3つ |
| 短3度 | 4つ | 長3度 | 5つ |
| 完全4度 | 6つ | ||
| 完全5度 | 8つ |
「鍵盤の数」はおまじないだと思って、
覚えてしまいましょう!
数学のむずかしい数式を覚えるよりは、
苦にならないですよね。
この①~③の工程をバッチリ頭に入れることが、
実際の問題を解くうえで最大の近道です。
今後スタートする
「問題の解きかた講座」で生かされますよ!
また、
問題を解いている過程で何かでつまづいたら、
この徹底講座に戻って
確認をするようにしてくださいね。






